Béton armé
Cette fiche décrit les principes de fonctionnement du béton armé. Un rappel de la notion d’efforts intérieurs est préalablement proposé. Il permet d’introduire le moment fléchissant, l’effort tranchant et l’effort normal. Ces notions sont ensuite exploitées pour exposer le principe du béton armé.
1 Notions préliminaires
1.1 Moment de flexion
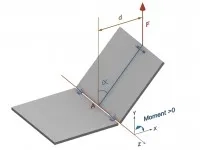
Réflexion à partir d’une poutre en flexion simple. Le moment d’une force par rapport à un point A est le produit de son intensité F par la distance d qui sépare le point de la droite support de la force. Cette distance est prise perpendiculairement à F. Sur la figure 1, le moment de F est porté par l’axe z. De plus, la rotation se produit suivant les z positifs. On le notera ainsi moment porté par z par rapport au point A, soit Mz/A.
![]()
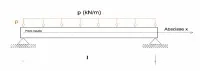
Le fléchissement de la poutre engendre l’apparition de forces internes non uniformes dans une section droite. Dans le cas d’une flexion engendrant une déformée dans le sens de la gravité, la partie supérieure de la poutre est soumise à des efforts internes de compression, tandis que la partie inférieure est soumise à des tractions (Fig. 3). Dans la plupart des structures, les déformations sont faibles et ne se voient pas à l’œil nu, ce qui n’exclut pas la présence de très grands efforts.

Les forces aux appuis sont calculées en appliquant le principe fondamental de la statique à l’équilibre de la poutre. Ici, puisque les forces sont symétriques par rapport à un axe vertical, les efforts des appuis sont égaux. Ils valent chacun pl/2.
Pour connaître l’amplitude de ces forces internes, on réalise mentalement une coupure de la poutre à une distance x de l’appui gauche.
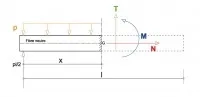
Si on considère la partie gauche de la poutre ainsi isolée, celle-ci doit être en équilibre sous l’action de l’ensemble des forces appliquées, dont celles qui agissent sur la section coupée. La matière de la partie conservée était sollicitée par la partie enlevée. Il faut donc remplacer l’action de la partie de droite par un ensemble d’efforts et de moment(s), qu’on appelle efforts intérieurs. Tout d’abord, on peut observer que les 2 sollicitations de sens contraire décrits sur la figure 3 créent un moment, M, qui est le moment de flexion, encore appelé moment fléchissant. Ensuite, dans le cas de la flexion, viennent s’ajouter un effort vertical, T, appelé effort tranchant et un dernier effort horizontal, N, appelé effort normal. On voit sur la figure 3 que Test intuitivement nécessaire pour équilibrer pl/2 (T sera ici de sens contraire à celui de la figure 4). Enfin, sur l’exemple, N est nul puisqu’il est seul à agir sur l’axe horizontal.
M, T et N sont des inconnues qui peuvent être calculées en écrivant les équations d’équilibre :
- la somme vectorielle des forces s’appliquant à la partie de poutre isolée est nulle, ce qui conduit à une équation suivant l’axe x, et une autre suivant y ;
- la somme des moments suivant l’axe z par rapport à un point quelconque est nulle.
En prenant le point G comme point de référence, on obtient une équation de moment où n’interviennent pas les effort T et N, puisqu’ils s’appliquent en G, et que, par conséquent, ils ont un bras de levier nul.
Dans l’exemple de la figure 4, la somme des efforts horizontaux étant nulle, l’effort normal N est alors nul.
La réaction d’appui d’intensité a un moment par rapport à G de
La charge répartie p a une résultante px et un bras de levier . Son moment par rapport à G vaut alors
L’équilibre en moment de la portion de poutre par rapport à G s’écrit alors : ![]()
![]()
![]()
![]()
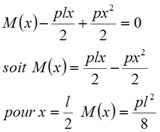
Il est important de noter que la portée est une grandeur déterminante du moment. Dans le cas de charges réparties, ce qui la plupart du temps est le cas, le moment évolue comme le carré de la portée. Il est par ailleurs proportionnel à la charge appliquée. L’effort tranchant doit être pris en compte dans le calcul des sections des poutres. Pour le calculer, on se sert de l’équation d’équilibre des efforts suivant l’axe y :
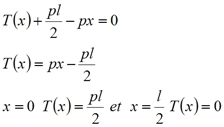
Les répartitions du moment fléchissant et de l’effort tranchant sont représentés sur la figure 5.
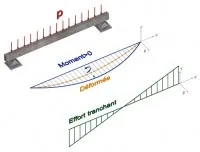
La répartition des moments fléchissant dépend des conditions d’appui. Dans l’exemple précédent, ce sont des appuis simples qui autorisent des rotations, ce qui élimine l’existence de moments aux appuis. Dans le cas d’encastrement, que ce soit pour une poutre console, ou une poutre bi encastrée, un moment - d’encastrement - apparaît aux appuis, ce qui modifie le diagramme de moment fléchissant (Fig. 6). Les moments étant des vecteurs suivant l’axe z dans notre exemple, la distribution du moment fléchissant est représentée sur un plan horizontal. On observe ainsi que la distribution de moment ne coïncide pas avec la déformée (à l’encastrement le moment est maximum et la déformée nulle), sauf dans quelques cas particuliers (poutre isostatique sur 2 appuis simples).
1.2 Contraintes dans les poutres en béton en flexion simple
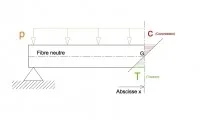
En reprenant l’élément précédent de poutre isolée soumise à la flexion simple, les sollicitations horizontales de la figure 3, qui génèrent de la compression en partie haute et de la traction en partie basse, sont en fait une modélisation de la répartition de pressions positives ou négatives dans la matière. Ces pressions sont appelées contraintes ; ici ce sont des contraintes normales car elles sont normales -perpendiculaires- à la section. Elles évoluent, pour la plupart des matériaux travaillant dans leur domaine de service, linéairement en fonction de y (Figure 7). Ces contraintes sont maximales et de sens opposé dans les fibres extrêmes de la section. Cela implique l’existence d’une fibre non contrainte que l’on nomme fibre neutre. Pour des poutres de sections symétriques par rapport au plan horizontal passant par z, la matière est sollicitée symétriquement avec la même intensité en traction et en compression et la fibre neutre se situe à mi-hauteur de la poutre. Pour des poutres de sections non symétriques (en Té, en U, etc.), la fibre neutre coïncide avec le lieu des centres de gravité des sections.
2 Béton armé
Résistance en compression et en traction du béton
Cherchons d’abord à expliquer pourquoi il existe rapport, de 10 à 20, entre la résistance en compression et la résistance en traction du béton.
Le béton appartient à la famille des céramiques, au sens large du terme, et a donc en traction un caractère fragile. Cette propriété s’observe dans la manière dont la matière se rompt. La rupture est dite fragile lorsqu’elle survient brutalement sans signe précurseur. On dit alors que le matériau est fragile. La fragilité n’est pas corrélée à la valeur de la résistance. Un matériau fragile peut être très résistant ou non. De plus, un matériau peut être fragile en traction mais pas en compression. Le caractère fragile du béton en compression apparaît par exemple vers les hautes résistances.
La propriété contraire est la ductilité. Dans le cas de la ductilité, le matériau se déforme jusqu’à des domaines irréversibles, qu’on dit plastiques, avant de se rompre. Dans le cas de l’acier de construction, la ductilité est liée à l’arrangement des atomes et à la possibilité de propagation de défauts. La microstructure cristalline de l’acier, la présence de dislocations (défauts) et la mobilité de ces dislocations sont à l’origine de la ductilité. D’autres mécanismes expliquent la ductilité pour d’autres matériaux. Pour les polymères, c’est plutôt l’enchevêtrement des longues chaînes moléculaires qui permettent de grands allongements plastiques. Le bois est quant à lui ductile en compression à cause du mécanisme de flambement successif des fibres.
Un matériau réputé fragile est le verre. Une autre propriété du verre est sa faible ténacité, caractérisée par la faible résistance à la propagation des fissures. Dès qu’une fissure se crée dans une plaque de verre, une faible augmentation de la sollicitation entraînera un fort risque de propagation de celle-ci jusqu’à la rupture de la plaque en 2 parties. Le sens de la sollicitation a ici une importance. La fissure se propagera facilement si on tend à en écarter les bords (traction perpendiculaire à la fissure), tandis qu’une compression tendant à refermer la fissure (compression perpendiculaire aux bords) n’aura pas d’effet, ou presque, sur sa propagation.
On peut résoudre à l’échelle de la structure un problème de fragilité du matériau. Les pare brise de voiture, ou les vitrages de sécurité, sont par exemple des structures multicouches intégrant des feuilles de butyral de polyvinyle (PVB) ayant un taux d’allongement important avant déchirure. L’arrêt de la progression des fissures par ces feuilles de PVB confère aux structures de vitrage feuilleté un caractère ductile. Un des intérêts du béton armé est d’avoir un comportement structurel ductile.
Pour expliquer la différence importante entre les résistances en traction et en compression du béton, il faut faire intervenir la présence de défauts et la propagation de ces défauts (ténacité). Pour le béton, ces défauts sont nombreux à l’échelle de la microstructure. Il s’agit des microfissures, des bulles d’air ou des interfaces entre la matrice cimentaire et les granulats. Les défauts initiaux vont évoluer ou non selon le sens de la sollicitation et son amplitude.
En traction, les défauts orientés perpendiculairement au sens de sollicitations, assimilés à des micro fissures, vont évoluer dès que les contraintes ont atteint la tenacité du matériau. Comme plus haut dans le cas du verre, ce sont les microfissures perpendiculaires aux contraintes de traction qui vont se propager. La rupture par traction d’un échantillon de béton se termine par la scission de l’échantillon en 2 parties pour des contraintes de quelques MPa. C’est donc la présence de défauts et la tenacité faible du béton non armé qui sont responsables de sa faible résistance en traction.
En compression, les fissures perpendiculaires aux contraintes vont se refermer sans se propager. Celles parallèles aux contraintes ne sont pas directement sollicitées et vont peu évoluer. La présence des défauts initiaux de la matière a donc beaucoup moins d’importance sur la rupture. C’est ce qui rend le béton, comme les céramiques, résistant en compression. A l’inverse, les aciers doux développent des déformations plastiques (irréversibles) importantes (ductilité) ainsi qu’une résistance à la propagation des fissures (ténacité). Les aciers doux possèdent alors les mêmes propriétés en traction et en compression.
Faiblesse du béton en flexion
La capacité en flexion d’une poutre en béton est donc faible, car dès que la contrainte de traction par flexion atteint la résistance en traction (Fig. 6), soit quelques MPa, une fissure va se propager verticalement et conduire à la ruine de la poutre. L’idée des ingénieurs et entrepreneurs de la fin du XIXème siècle (Monier, Hennebique, Considère, etc.) a été de placer des barres d’aciers dans les zones où la matière est sollicitée en traction. Cette disposition est pertinente et durable grâce au respect de 3 principes :
- les contraintes de traction du béton sont transmises aux aciers par des contraintes tangentielles, grâce à une très bonne adhérence entre l’acier et le béton ;
- les coefficients de dilatation du béton et de l’acier sont très voisins, c’est-à-dire de l’ordre de 1/100ème de mm/m/°C. Cette coïncidence élimine tout risque d’apparition d’autocontraintes lors de variations de longueur d’origine thermiques ;
- les aciers sont protégés de la corrosion dans le béton sain car le pH y est de l’ordre 13,5, c’est-à-dire très basique. Cette protection des aciers est à la base de la durabilité du béton armé (voir fiche durabilité).
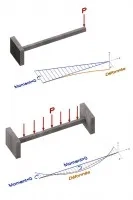
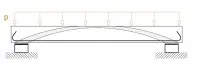
Une description du principe du béton armé peut être résumée sur la figure 8. On y décrit un fonctionnement en arc-tirant. La zone en gris schématise le parcours des contraintes de compression dans le béton. Cette zone forme un arc interne. La poussée de cet arc est reprise par les aciers de traction placés en partie inférieure de la poutre. Néanmoins, on préfère modéliser le béton armé en réalisant des coupures fictives de la poutre en plusieurs sections choisies, et en se servant du moment fléchissant pour la détermination de la quantité d’armatures nécessaire (Fig. 9). Le moment fléchissant est, pour les structures isostatiques, indépendant du matériau, on le calcule par les équations de la statique. L’effort de traction dans l’acier est ensuite calculé en égalant le moment fléchissant avec le couple des efforts internes. A partir de cet effort et de la contrainte admissible dans l’acier (autour de 350 MPa), on calcule la section d’acier nécessaire.

2.1 Contraintes normales dans les poutres en béton armé
La faible valeur de résistance du béton en traction conduit les ingénieurs à la négliger et à considérer que la structure en flexion doit fonctionner même lorsque les zones de béton en traction sont fissurées. Cela permet de solliciter les barres d’acier dans des domaines de déformations qui permet de les exploiter efficacement. Une contrainte de service de l’acier de 300 MPa, par exemple, conduit à une déformation de 300/210000 = 0,001 m/m, alors que le béton fissure pour une déformation en traction plus de 6 fois plus faible. On s’aperçoit ainsi que le béton enrobant l’acier est forcément fissuré au taux de travail de service de l’acier (Fig. 10). Inversement, si l’on voulait empêcher toute fissuration du béton, on serait conduit à surdimensionner la section des aciers afin d’en limiter la déformation. Cela conduirait à faire travailler l’acier à un taux de contrainte si faible que la technologie du béton armé ne serait plus intéressante. Pour ne pas faire fissurer le béton, on limiterait la déformation de l’acier approximativement à 0,00015 m/m, soit 150.10-6m/m. La contrainte de traction dans l’acier serait réduite à 210 000 * 0,00015 = 31,5 MPa.
On aboutit à une distribution des contraintes dans une section en béton armé conforme à celle de la figure 11, dans laquelle les contraintes de compression sont équilibrées par l’effort de traction dans les barres d’acier. Cette configuration est différente de celle de la figure 7, et montre que le béton armé est véritablement un matériau composite. remarquons enfin que l’axe neutre dans les poutres en béton armé n’est pas à mi hauteur, mais se trouve décalé vers la zone de béton en compression.

2.2 Des contraintes de traction inclinées
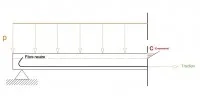
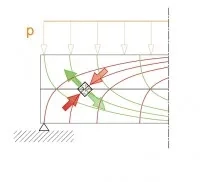
La figure 12 illustre le fait que les lignes des contraintes de compression, en rouge, et de traction, en vert, forment un réseau de courbes orthogonales. Le réseau des courbes rouges est à rapprocher de la modélisation de l’arc de la figure 8. Cette répartition a été démontrée tant expérimentalement que théoriquement pour les matériaux homogènes élastiques. On observe aussi qu’au voisinage de l’appui, là où l’effort tranchant est maximum, le matériau est sollicité en traction suivant une facette inclinée par rapport à l’horizontale (Figure 13).
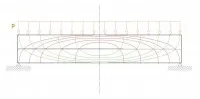
Ces contraintes présentent le risque de création de fissures perpendiculaires aux tractions. Cette zone sensible nécessite des armatures, appelées cadres, que l’on pourrait incliner pour en optimiser l’effet, mais que l’on place en fait, la plupart du temps, verticalement. La répartition horizontale des cadres est calculée en fonction de l’évolution sur l’axe horizontal de l’effort tranchant. Pour une poutre sur 2 appuis, chargée uniformément, la distance entre cadres augmente lorsque l’on s’éloigne de l’appui (Figure 14). Les barres horizontales supérieures sont des armatures de montage permettant le maintien des cadres.
2.3 Pré dimensionnement
La stratégie de l’ingénieur est de fixer d’abord la taille extérieure des éléments et de calculer ensuite les armatures nécessaires à l’équilibrage des efforts intérieurs (moment fléchissant, effort tranchant, effort normal). Pour une poutre fléchie, une géométrie trop petite conduit à introduire plus d’acier. Pour un moment fléchissant donné, lorsque la hauteur de la poutre diminue, le bras de levier du couple des efforts internes aussi, il faut alors augmenter l’effort de traction des aciers, donc le nombre de barres. A l’inverse, lorsque la hauteur de la poutre augmente, le bras de levier du couple des efforts internes augmente, et l’effort apporté par l’acier diminue, donc le nombre de barres nécessaires aussi. Il arrive de devoir placer des aciers supplémentaires dans la zone comprimée lorsque le béton ne peut pas supporter les efforts internes de compression. Bien que ce soit assez courant, cette solution n’est pas toujours la plus économique. Son application est de plus limitée par la possibilité de bétonnage. Dans des cas extrêmes, les aciers nécessaires sont si nombreux que le bétonnage devient une opération difficile. Les photos des poutres en « X » de l’école d’architecture de Lille illustrent ce propos.
Des ratios plus ou moins précis permettent de fixer des hauteurs de poutres convenant à des chargements de type habitat (charges d’exploitation de 1,5 kN/m2) et, s’il s’agit de planchers, en fixant des entraxes courants de 6 à 8 m entre poutres.
Ainsi, la hauteur des poutres isostatiques est environ 1/10ème de leur portée. Pour les poutres hyperstatiques, la hauteur est plutôt de 1/15ème de la portée. La hauteur des poutres intègre l’épaisseur des dalles. Ainsi, pour une poutre de 0,6 m de hauteur supportant une dalle pleine en béton armé de 0,2 m d’épaisseur, la retombée visible de la poutre sera alors de 0,4 m. La hauteur des dalles est de l’ordre de 1/30ème à 1/35ème de leur portée.
Les éléments travaillant essentiellement en compression (poteaux et voiles) sont pré dimensionnés en fixant une contrainte de service dans le béton. La descente de charges est une opération préalable consistant à additionner pour chaque niveau de la construction les efforts verticaux qui transitent dans l’élément. La somme de ces efforts sur l’élément, divisée par la contrainte de service, donne la section de béton nécessaire. Par exemple un effort de compression de 1000 kN (ou 1 MN soit 100 tonnes), dans un poteau réalisé avec un béton dont la contrainte de service est de 10 MPa (10 MN/m2), nécessite une section de 1/10 = 0,1 m2, soit une section carrée de 32 cm de côté ou circulaire de 36 cm de diamètre. N’oublions pas que les éléments comprimés sont soumis à une vérification de non flambement. Ce risque existe pour les poteaux en béton de grande hauteur.
BIBLIOGRAPHIE
Rémy Mouterde, François Fleury, (2007) Comprendre simplement la résistance des matériaux - La structure, principes et enjeux de la conception, Editions du Moniteur, Paris.
André Coin, (1991), Ossature des bâtiments - Bases de la conception, différentes catégories d’ouvrages élémentaires, annexes sur l’isolation et la sécurité, Eyrolles, Paris.
-
R&D - Valorisation déchets textiles et résistance du béton
-
R & D - Capturer le carbone
-


COMMENTAIRES
3 COMMENTAIRES